Броенето - основа в математиката

В последно време все по-често се чуват констатации от родители и учители, които звучат по-общо по този начин: „Детето не може да смята, да брои. По четене и писане се справя, но по математика е много зле. Не разбирам как да работя с него. Обяснявам, показвам и пак нищо... Когато трябва да направи преброяване, той все се връща и брои отново и отново или губи мястото на преброения предмет и го преброява два пъти, брои пръстите си, пресмята и пак грешно...”

Много често математиката се оказва трудно разбираема за децата и това особено се забелязва, когато те започнат да прилагат действия събиране и изваждане. За децата и учениците с дислексия и диспраксия се оказва още по непосилно да разберат принципите на математиката. Много от децата дълъг период от време (а понякога и като възрастни) се затрудняват да преброяват и пресмятат на пръстите си (защото там единствено се научават, че един пръст е вече преброен и не го броят повторно).

При ученици, които се затрудняват със събиране и изваждане, се оказва се, че всички те са имали затруднения с разбирането на количествата и преброяването им.  Като по-големи те споделят, че за тях броенето не носи и никога не е носило някакъв смисъл и не намират необходимост да го правят. Те извършват броенето механично, казват едно след друго числата и не се замислят какво означават.

Броенето е първата най-важна стъпка и е базово в развитието на математическите умения. Много важно е от ранна възраст децата да разберат принципите на броенето и връзката му с различните области от живота, да разберат защо броенето има смисъл. Това е в основата на изграждането на детското абстрактно мислене за числата. Когато навлизаме в света на числата, разбираме, че те се използват в различен контекст. Деца с бедна представа за количествата, започват да развиват увереност и да разбират необходимостта от броенето, когато им се дава възможност да броят/боравят с реални предмети. Когато нещо премине през действието (ръцете),  то се разбира и запомня по-лесно. 

Има три вида преброяване, които са основани на различни модели, с които е полезно да се занимават децата. Тези модели са линеен, стъпаловиден и схематичен.

Линеен модел за броене (линеен броен модел)

Една от основните цели за разбирането и добиване на увереност в пресмятането е децата да се научат да откриват (т.е. да станат по-добри в откриването на) количествата около себе си и да ги съотнасят помежду им (повече, по-малко и т.н.).

Трудностите свързани с разбирането на количествата (числата) идват от това, че детето просто не е научено как да брои. В ранна детска възраст често се набляга на „рецитирането” на числата. Например в много песнички, залъгалки, броилки  се брои. Именно това броене е „рецитиране” на числата, без да има разбиране на множествата и на количествата.

За да се преодоляват по-лесно затрудненията по математика, е необходимо  децата да натрупат достатъчно опит за преброяване на обекти по определен начин, за да могат да обработват общи количества. Например: „Колко патета има в това голямо патешко семейство?”.

По този начин вниманието се фокусира върху групата, а не върху отделните обекти. Децата трябва да се насърчават да броят и да виждат обектите по организиран, ритмичен начин. 

Това помага думите и предметите да се синхронизират. (напр.: „едно” се отнася към едно пате, „две” към две патета и т.н.). Хубаво е броенето да се извършва, както в редици, така и в колони, и децата да се приканват да броят и по двата начина – множеството подредено в колона или редица.

За разбиране на количествата е добре да се използват няколко прости подхода:

• Накарайте децата да прогнозират разхвърляни множества от единици (купчини от обекти).
• Да преброяват предметите в последователност. Това помага да се съсредоточат върху реалната многочисленост на преброяваното множество.
• Да вземат предположено количество от множеството, да кажат колко са взели, да проверят чрез преброяване дали отговаря на зададения брой и да го коригират, ако е необходимо (т.е., ако е взело 7, а трябва да е взело пет – да го поправи).

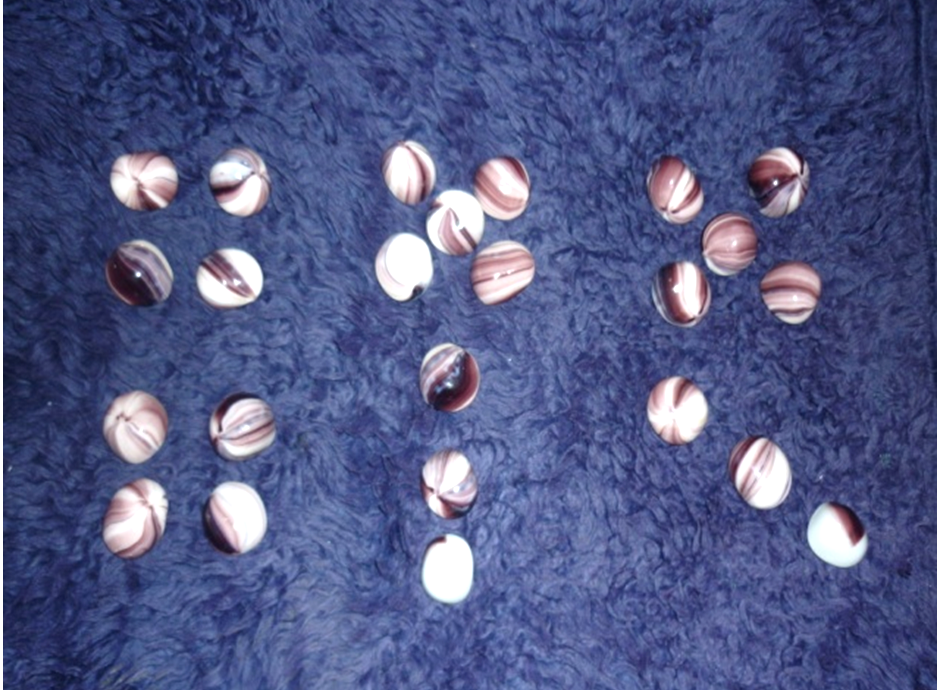
Добре е преди да отговори, детето да направи кратка пауза, за да може да обмисли отговора си, да вникне в него и тогава да го изкаже на глас. Възможно е детето първо да каже грешен брой на предметите, които е взело, и след това да каже верния.

На по-късен етап, може да се кара детето да казва колко е разликата и по този начин да го подготвим за изваждане на числа. 

Важно е да знаем, че е грешка да караме децата да броят без да ги питаме колко обекта има в множеството (групата). Състезателните игри за събиране с прости числови редици е отличен начин за фокусиране на вниманието на детето върху числата.

Стъпаловиден модел

Този модел дава възможност да се разбере връзката между числата в бройна последователност. Основен принцип е всяко следващо число в последователността на броене да е с едно повече от предишното. Изгражднето на стълбица води до разбиране на взаимоотношенията между числата (стълбичката може да се направи още с кубчета, строител, като мрежа в тетрадката).

Стълбичката може да е цветна и реална. От детето се изисква да подреди в последователност безразборно дадените кубчета или други реални предмети. По-сложен вариант е да подреди липсващата/непълна последователност от кубчета. 

Схематичен модел

Същността на този модел е схематично представяне на числата.

За числата над 10 е хубаво да се правят числови структури, които са базирани на числовите структури за числата до 10.

Линейните образи за числата от 5 до 10 се оказват доста неясни и трудни за разбиране. В тези случаи много полезно е децата да се запознаят с образи на числата по-големи от 5, които са базирани на образи за числата до пет, които веднага се разпознават. Ако детето разпознава пет по този начин, то ще разпознае по-лесно числото осем или седем, ако се представи така:

Този модел е подходящ и при работа с числа по-големи от 10. За целта стандартните числови модели могат да се построят, да нарисуват цифрата като рисунка. Например: 

Децата интуитивно напасват други подредби на основните числа до 10. Към моделите, които са им известни, те измислят свои собствени.

Схематичните модели осигуряват образи, които могат да отговорят на абстрактните думи за числата и символите до 10, което е особено подходящо за числата от 5 до 10. Децата, които са запознати добре с числовия модел, започват да виждат числата в различни конструкции, които могат да бъдат построени или развалени и отново построени (т.е. започват да правят собствени комбинации, като развиват образи за числата, базирани на компоненти).

Те виждат всяко число като част от нещо друго, а не само за себе си. Може да се накара детето да измисли собствени схеми на числата или да избере такива, които са най-достъпни за него.

Тази предварителна работа е особено важна за деца и ученици със специални образователни потребности като когнитивна работа с повтарящи се числови групи, което ще подпомогне разбирането на действия като умножение и деление.

Така че бройте и създавайте реална представа и образи у децата от ранна възраст за множества, количества и цифри. Това ще ги направи по-уверени в изучаването на математиката.